CANTIDAD DE MOVIMIENTO O MOMENTUM LINEAL: 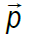
Históricamente el concepto de cantidad de movimiento surgió en el contexto de la mecánica newtoniana en estrecha relación con el concepto de velocidad y el de masa. En mecánica newtoniana se define la cantidad de movimiento lineal como el producto de la masa por la velocidad:
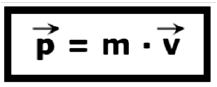

La idea intuitiva tras esta definición está en que la “cantidad de movimiento” dependía tanto de la masa como de la velocidad: si se imagina una mosca y un camión, ambos moviéndose a 40 km/h, la experiencia cotidiana dice que la mosca es fácil de detener con la mano mientras que el camión no, aunque los dos vayan a la misma velocidad. Esta intuición llevó a definir una magnitud que fuera proporcional tanto a la masa del objeto móvil como a su velocidad.
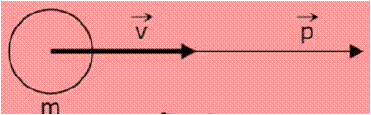
El momentum lineal p es una cantidad vectorial, de igual dirección y mismo sentido que el vector velocidad v, como muestra la figura, donde se observa el momentum y la velocidad de una masa m. Por la definición en el SI la unidad de medida del momentum lineal es Kg m/s

IMPULSO: 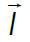
 Supongamos que se quiere desplazar una pelota de golf, para tal efecto se debe aplicar una fuerza mediante el palo de golf. La fuerza que se requiera va depender del alcance que se desee obtener en la pelota, es decir se debe impulsar la pelota. Otro factor que influye es el tiempo de contacto, de aplicación de la fuerza. De esta forma, entre mayor sea el tiempo en que apliquemos dicha fuerza, la pelota adquirirá una mayor velocidad.
Supongamos que se quiere desplazar una pelota de golf, para tal efecto se debe aplicar una fuerza mediante el palo de golf. La fuerza que se requiera va depender del alcance que se desee obtener en la pelota, es decir se debe impulsar la pelota. Otro factor que influye es el tiempo de contacto, de aplicación de la fuerza. De esta forma, entre mayor sea el tiempo en que apliquemos dicha fuerza, la pelota adquirirá una mayor velocidad.
En consecuencia, la variación de la velocidad de un cuerpo dependerá tanto de la fuerza aplicada como del tiempo de aplicación.
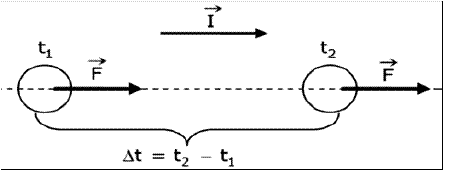
Llamaremos impulso (I) al producto entre la fuerza (F) que se aplica y el tiempo (Δt) que apliquemos dicha fuerza, es decir:

En el S.I. la fuerza se mide en N (Newton) y en el tiempo en s (segundos), por lo que el impulso tendrá unidades en el S.I. de unidades de N ∙ s.
Observemos en la figura, que I es un vector que tiene la misma dirección y el mismo sentido que F.
 RELACIÓN ENTRE IMPULSO Y MOMENTUM LINEAL
RELACIÓN ENTRE IMPULSO Y MOMENTUM LINEAL
Cuanto mayor sea la fuerza que actúa sobre un objeto, mayor será el cambio de la velocidad y, en consecuencia, mayor será el cambio en la cantidad de movimiento.
Pero hay algo más que importa cuando cambia la cantidad de movimiento: el tiempo, es decir, durante cuánto tiempo actúa la fuerza. Aplicar una fuerza durante un corto tiempo a un automóvil parado y se producirá un cambio pequeño de su cantidad de movimiento. Aplicar la misma fuerza durante largo tiempo y resultará un mayor cambio de su cantidad de movimiento. Una fuerza sostenida durante largo tiempo produce más cambio de cantidad de movimiento, que la misma fuerza cuando se aplica durante un breve lapso. Así, para cambiar la cantidad de movimiento de un objeto importan tanto la magnitud de la fuerza como el tiempo durante el cual actúa la fuerza.
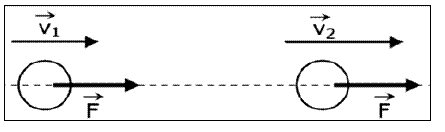
Cuando se golpea una pelota de golf en el campo de juego, una gran fuerza F actúa sobre la pelota durante un corto intervalo de tiempo Δt, haciendo que ésta se acelere desde el reposo hasta una velocidad final. Es en extremo difícil medir tanto la fuerza como la duración de su acción; pero el producto de ambas, F · Δt, puede calcularse en función del cambio de velocidad resultante de la pelota de golf.
En la figura un cuerpo de masa m, se mueve con una velocidad vi. Si una fuerza F, constante, actúa sobre el cuerpo durante un intervalo de tiempo Δt, observaremos que su velocidad sufrirá una variación, pasando a ser vf al final del intervalo.
A partir de la segunda ley de Newton, sabemos que
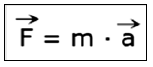
usando la definición de aceleración
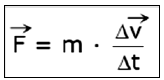
Multiplicando por Δt se obtiene:

de donde se tiene

Se observa:
F · Δt, Representa el impulso I que recibió el cuerpo
m · vf, Representa la cantidad de movimiento del cuerpo, P2, al final del intervalo Δt
m · vi, Representa la cantidad de movimiento del cuerpo, P1, al inicio del intervalo Δt
Como:
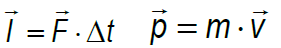
Reemplazando:

es decir:

Esta es la relación que existe entre el impulso y el momentum, es decir, el impulso es el responsable de la variación en el momentum del cuerpo.
Podemos distinguir con facilidad 2 tipos de choques.
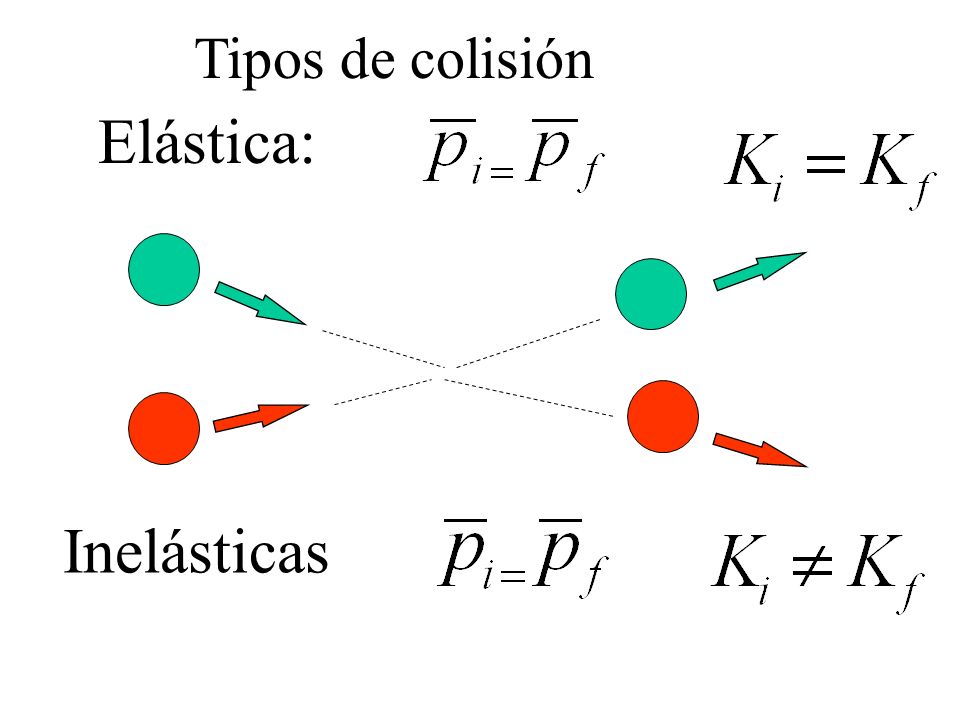
CHOQUES ELÁSTICOS
En física, en el caso ideal, una colisión perfectamente elástica es un choque entre dos o más cuerpos que no sufren deformaciones permanentes debido al impacto. En una colisión perfectamente elástica se conservan tanto el momento lineal como la energía cinética del sistema. Claro está que durante una colisión, aunque sean de dos sólidos, no se puede considerar perfectamente elástico ya que siempre hay una deformación.




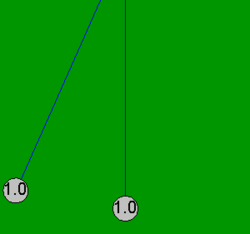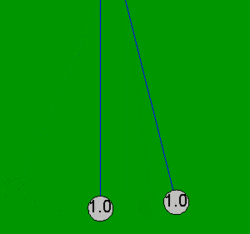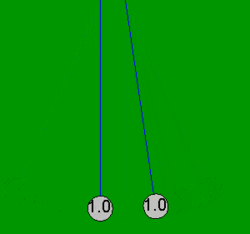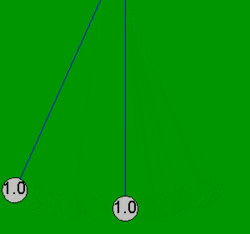

CHOQUES INELÁSTICOS
Las colisiones en las que la energía no se conserva producen deformaciones permanentes de los cuerpos y se denominan colisiones inelásticas. Lo podemos definir como un choque en el cual la energía cinética se pierde o no se conserva. Como consecuencia los cuerpos que se chocan sufren deformaciones en su masa y aumento de su temperatura.
En un choque inelástico (o choque plástico) los cuerpos presentan deformaciones luego de su separación, esto es una consecuencia del trabajo realizado. En el caso ideal de un choque perfectamente inelástico, los objetos en colisión permanecen pegados entre sí. El marco de referencia del centro de masas permite presentar una definición más precisa. En los choques inelásticos la energía cinética no se conserva, ya que parte de ella es "usada" para deformar el cuerpo.
Es por esto que se puede decir que en el choque inelástico la energía se ve reducida debido a la incapacidad de regresar a su estado original los cuerpos.

De tal manera que en el choque inelástico habrá transformación de energía mientras en contraste, el choque elástico la mantendrá constante.
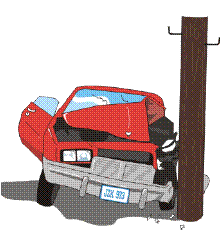

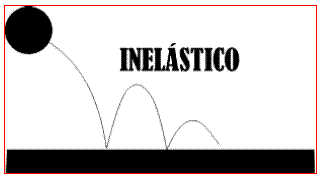
CHOQUE PERFECTAMENTE (TOTALMENTE) INELÁSTICO
En los choques totalmente inelásticos, los cuerpos que chocan se mueven tras la colisión con la misma velocidad de manera que parecen estar pegados y se comportan como un único cuerpo. En este tipo de choques se conserva la cantidad de movimiento pero toda la energía puesta en juego en el choque se transforma en calor o deformación y no se recupera para el movimiento.
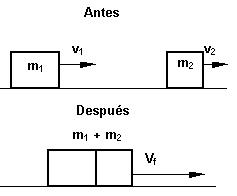


Ejercicios de Colisiones
1) Una bola de bolos de 7 kg choca de frente con un pin de 2 kg. El pin vuela de frente a una velocidad de 3 m/s. Si la bola sigue adelante con una velocidad de 1,8 m/s, Cual es la velocidad inicial de la Bola? Despreciar rotación de la bola

m1v1i+ m2v2i = m1v1f+ m2v2f.
(7 kg)(vi) + (2 kg)(0) = (7 kg)(1.8 m/s) + (2 kg)(3 m/s)
vi = 2.66 m/s
2) Un carro que va hacia la derecha (rojo), tiene una masa m1 = 1500 kg, lleva una velocidad inicial v1i= 50 millas/hora, choca de frente contra otro carro que va hacia la izquierda (azul), tiene una masa m2=1800 kg, a) hallar la velocidad con la que termina el carro azul.

m1v1i + m2v2i = m1v1f + m2v2f.
(1500kg)(50m/h) + (1800kg)(50m/h) = (1500kg)(50m/h) + (1800kg)(50m/h)
3) Un carro que va hacia la derecha (rojo), tiene una masa m1 = 1500 kg, lleva una velocidad inicial v1i= 50 millas/hora, choca por detrás al carro (azul), tiene una masa m2=1800 kg, y lleva una v2i = 20 millas/hora, a) hallar la velocidad con la que termina el carro rojo.

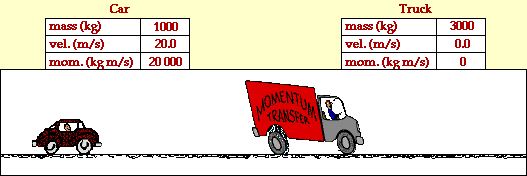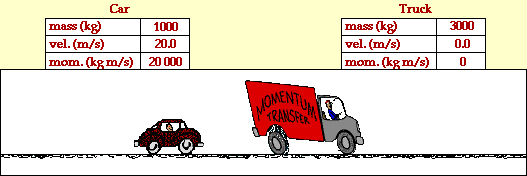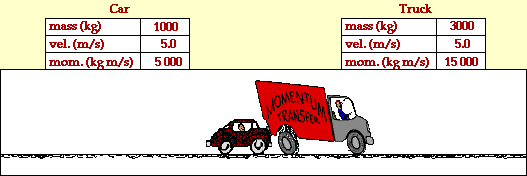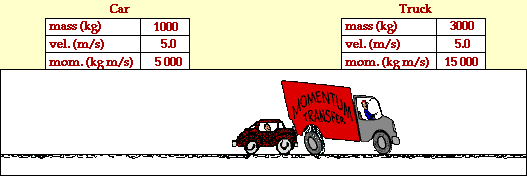














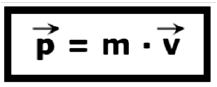



 Supongamos que se quiere desplazar una pelota de golf, para tal efecto se debe aplicar una fuerza mediante el palo de golf. La fuerza que se requiera va depender del alcance que se desee obtener en la pelota, es decir se debe impulsar la pelota. Otro factor que influye es el tiempo de contacto, de aplicación de la fuerza. De esta forma, entre mayor sea el tiempo en que apliquemos dicha fuerza, la pelota adquirirá una mayor velocidad.
Supongamos que se quiere desplazar una pelota de golf, para tal efecto se debe aplicar una fuerza mediante el palo de golf. La fuerza que se requiera va depender del alcance que se desee obtener en la pelota, es decir se debe impulsar la pelota. Otro factor que influye es el tiempo de contacto, de aplicación de la fuerza. De esta forma, entre mayor sea el tiempo en que apliquemos dicha fuerza, la pelota adquirirá una mayor velocidad.



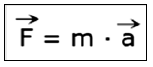
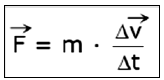




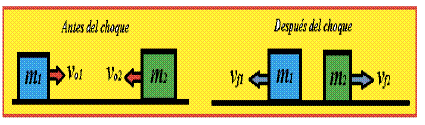

 Un choque físico o mecánico es percibido por una repentina aceleración o desaceleración causada normalmente por un impacto, por ejemplo, de una gota de agua, aunque también una explosión causa choque; cualquier tipo de contacto directo entre dos cuerpos provoca un choque. Lo que mayormente lo caracteriza es la duración del contacto que, generalmente, es muy corta y es entonces cuando se transmite la mayor cantidad de energía entre los cuerpos.
Un choque físico o mecánico es percibido por una repentina aceleración o desaceleración causada normalmente por un impacto, por ejemplo, de una gota de agua, aunque también una explosión causa choque; cualquier tipo de contacto directo entre dos cuerpos provoca un choque. Lo que mayormente lo caracteriza es la duración del contacto que, generalmente, es muy corta y es entonces cuando se transmite la mayor cantidad de energía entre los cuerpos.


